積分を利用した重心の求め方 back 定積分と面積 いろいろな図形の重心の位置を積分を利用して求めることで、積分に興味をもち、 単元の有用性を感じることが、この教材のねらいである。 重心を求める公式がある。これは、図形の面積をSとしたとき、剛体の重心(2 a) このL字型の 板の重心 2 つ の 四 角 形 の 和 質量比 2:1 重心 重心 2 1 3つの正方形の和と考えてもよい 工学院大学の学生のみ利用可:印刷不可:再配布不可 (c)加藤潔18 9扇形 P11 弓形 P11 楕円 P11 放物形 P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸の
高中物理教材內容討論 質心的推導
扇形 の 重心
扇形 の 重心-2 重心の求め方:モーメントの釣り合いを考える 早速、重心を求めていきましょう。 方針としては、 物体にかかる力の作用線を書き、モーメントの釣り合いから重心を求めます。 モーメントとは、回転する力のこと です。 基準点から見て、右周りか左周りに回転し、 基準点からの距離×力2 重心の求め方:モーメントの釣り合いを考える 早速、重心を求めていきましょう。 方針としては、 物体にかかる力の作用線を書き、モーメントの釣り合いから重心を求めます。 モーメントとは、回転する力のこと です。 基準点から見て、右周りか左周りに回転し、 基準点からの距離×力


課業輔導中心 錐體的體積和表面積
重心の定義通りに地道にやれば解けますよ。 扇形の重さを仮に1 とすると、面積は πr^2(α/(2π))=αr^2/2 だから単位面積当たりの重さρ=2/(αr^2) で重心は、扇形を微小質量の集まりと考え、位置 (x, y)に微小質量dm があるとすると、重心は、教科書の公式通りに扇形 P11 弓形 P11 楕円 P11 放物形 P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸の切り抜かれた円盤の重心 下図に示すように, 密度が一様で半径 \( r \) の円盤1から, それに内接する半径 \( \frac{r}{2} \) の円盤2を切り抜いた物体について, 次の問に答えよ
扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。このページでは、扇形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。1)重心を通らない回転軸の I は,重心を通 る平行な軸に関する I から決まる。 (p84平行軸の定理) 2)重心を通る任意の軸に関する I は3つの 主慣性モーメントから決まる。 (514節:慣性テンソル) → 以下で説明扇形が大きければ大きいほど大きくなる。 おうぎ形パワーとは、 「同じ半径の円」に対して「扇形」がどれくらいの割合になっているか?? ということを表したものなんだ。 この割合を計算するためには、 「扇形の中心角」が360°中どれだけ大きいか?
図心と重心 物体は多くの質点の集まりであり各質点はその質量に 比例する重力の作用線を受ける。 この平行線の合体を物体の重量といい この着力点を重心という。あたっては足位による影響を除外するために30°扇形足 位を用いた。〔図1〕は,そ の1例 を示したが,種 々な足 位によって動揺の重心図に差が生じ,あ るものはX軸 に 図1 足位による重心動揺軌跡の諸相 RG Romberg足 位,30G 30°扇形足位,重心の定義通りに地道にやれば解けますよ。 扇形の重さを仮に1 とすると、面積は πr^2(α/(2π))=αr^2/2 だから単位面積当たりの重さρ=2/(αr^2) で重心は、扇形を微小質量の集まりと考え、位置 (x, y)に微小質量dm があるとすると、重心は、教科書の公式通りに



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积


高中物理教材內容討論 質心的推導
は、数式によっても重心を求めることができま す。図のような物体は、AとBに分け、それぞ れの対角線の交点によって重心G1とG2を求め ます。Aの質量をW1、Bの質量をW2とすると、 Aの重心G1から物体の重心Gまでのaの長さ及面的重心之求法 一、簡單面積之重心 1矩形面積之重心 正方形、長方形、菱形之重心,在其對應兩邊中點聯線之交點上,或其對角線之交點上,如圖所示。 2三角形面積之重心構造計算の基礎 ー構造力学の基本ー 東京都市大学 都市工学科教授皆川勝



御所実業高校 機械工学科 の日記 第22回 重心の答え合わせ



厂家直销电子体重秤龙剑扇形电子称家用体重秤促销礼品秤正品 阿里巴巴
《参考》 1)三角形の面積と重心 2)扇型の面積と重心 3)角錐台の体積と重心 r大きい方の扇形をa、小さい方の扇形をbとして、 (aの面積×aの重心-bの面積×bの重心)÷ (aの面積-bの面積)でやったのですが全然違う数値にな りました。扇形の半径r、角度θ、面積がSです。 扇形の面積と円の面積、扇形の角度と円の角度の比率は同じなので、 S:πr 2 =θ:2π S2π=πθr 2 S=r 2 θ/2 です。扇形の面積が角度の大きさに比例することを利用して導いています。扇形の弧の長さLも、同様の関係を


一 与圆有关的各种图形的面积 几何重心与转动惯量计算公式



この問題の半径rと中心核aの扇型の重心の位置を求める問題がさっぱりで 数学 教えて Goo



扇形与圆锥思维导图 第1页 一起扣扣网


确定不规则形状物体重心的方法 腾讯视频



Pk Ckcos6 半圓形的質心



实验四纸和纸板撕裂度的测定下载 Word模板 爱问共享资料



扇形与圆锥思维导图 第1页 一起扣扣网



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积
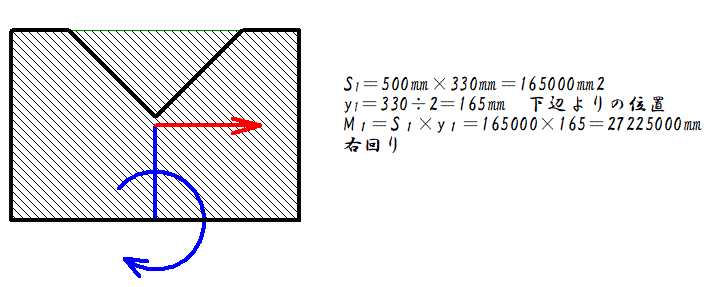


御所実業高校 機械工学科 の日記 第22回 重心の答え合わせ



Ppt 第四章空间力系powerpoint Presentation Free Download Id



Matlab等距扇形反投影分析 尚码园


扇形の重心の求め方 積分 半径r 内角60度の薄板上の扇形の重心の Yahoo 知恵袋


扇形怎么变成圆锥的图 第1页 要无忧健康图库
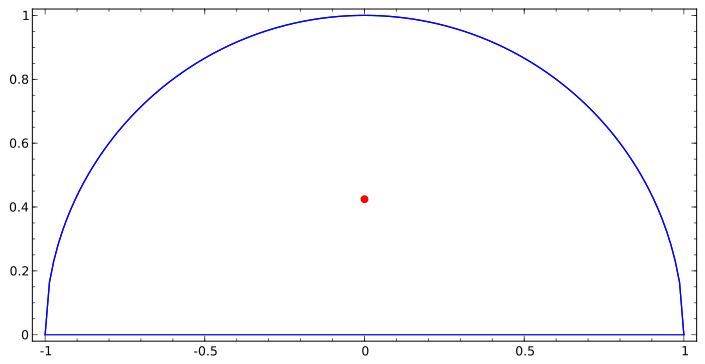


重心列表 维基百科 自由的百科全书



Matlab等距扇形反投影分析 趣讀


国际教科书 伦巴第1讲 移动基本步 扇形 Basicmovement


面的重心求法



扇形重心位置计算 三人行教育网 Www 3rxing Org


扇形の重心位置 X座標にあるとします の求め方を教えていただ Yahoo 知恵袋



你跟大神的差距就在這 角色人物立繪構圖與重心的繪畫參考 壹讀


課業輔導中心 錐體的體積和表面積
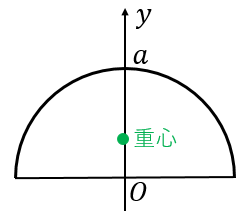


半円の重心の位置を求める公式 具体例で学ぶ数学



扇形重心位置计算 三人行教育网 Www 3rxing Org


二重积分计算问题



扇形与圆锥思维导图 第1页 一起扣扣网



Pk Ckcos6 半圓形的質心



M Sudo S Room 円弧 及び 扇形の重心


3 5 重心 形心和静矩



物理 力学 物理に関する質問 勉強質問サイト



三角形重心坐标公式推导 Weixin 的博客 Csdn博客 三角形重心坐标公式推导



初中一道特別典型的扇形面積計算類例題 每日頭條
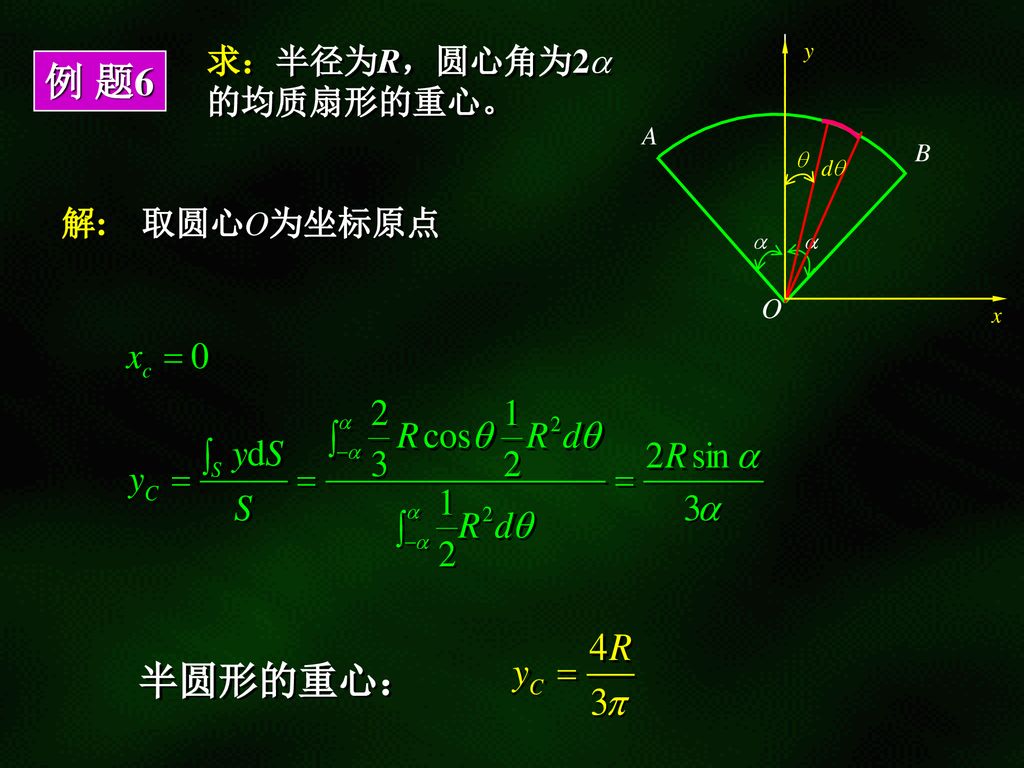


第6章空间力系和重心 空间任意力系的平衡方程 空间约束和约束反力 空间力系平衡问题举例 重心 结论与讨论 Ppt Download


面的重心求法


几何画板课件和微课制作入门到进阶教程d8验证三角形的重心坐标公式 知识 名师课堂 爱奇艺


扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积



Fzu 1330 Center Of Gravity 计算几何 求扇形重心 Weixin 的博客 Csdn博客



圆脸 方脸千万别戴这些耳饰 不然脸大一圈 每日头条
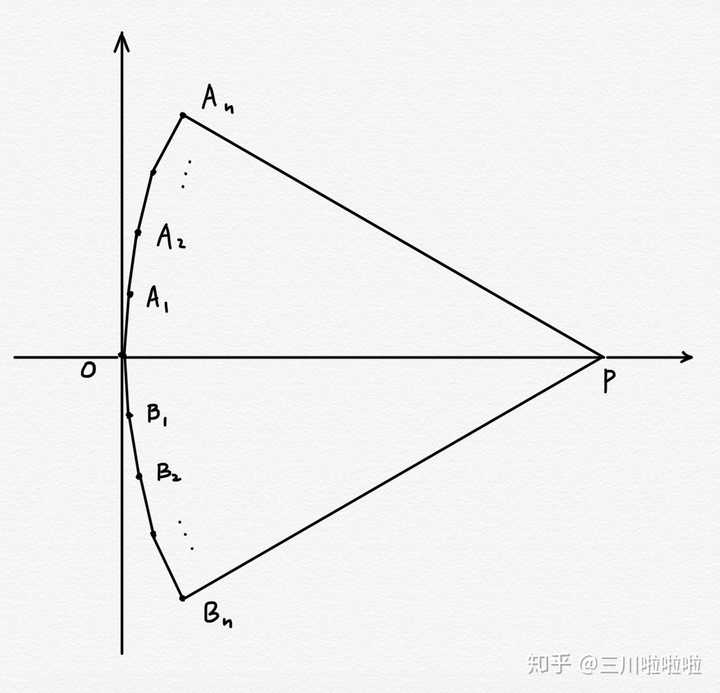


平面有界凸集上的点到其重心的最大距离是其直径的比例的上界是多少呢 三川啦啦啦的回答 知乎


新網頁1



扇形重心位置计算 三人行教育网 Www 3rxing Org
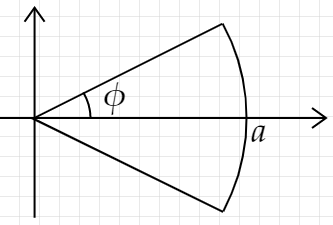


積分による重心位置の求め方 わすれなぐさ


建筑力学 西南大学网络教育学院



Pk Ckcos6 半圓形的質心



第十五届应用竞赛初赛试题及参考解答下载 Word模板 爱问共享资料
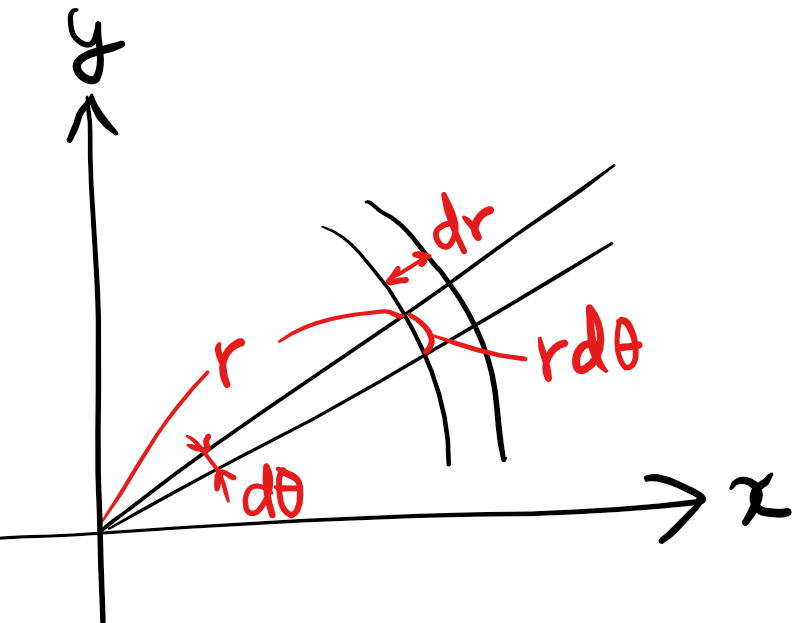


積分による重心位置の求め方 わすれなぐさ



扇形の重心を積分で ウソの国ー詩と宗教 戸田聡



人物立绘画法教程 学院 摸鱼网 S っ D っ让世界更萌 Mooyuu Com


3 5 重心 形心和静矩



16 0404号 レシプロエンジンのクランク軸 Astamuse



機械力學 上 Ch03 Jibao 洞悉教材的趨勢


扇形怎么变成圆锥的图 第1页 要无忧健康图库



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积


扇形计算公式 钢筋计算公式 光通量计算公式 箍筋长度计算公式 Www Shianwang Com


下の扇形みたいな図形の重心を求めたいです 大きい方の扇形をa 小さい方の扇 Yahoo 知恵袋



Pk Ckcos6 半圓形的質心


扇形计算公式 钢筋计算公式 光通量计算公式 箍筋长度计算公式 Www Shianwang Com



24 7 弧长与扇形面积 初中电子课本


3 5 重心 形心和静矩
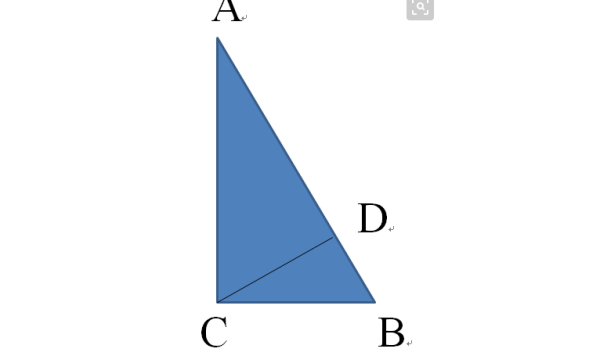


求直角三角形的重心 等腰三角形的重心 等边三角形的重心 等腰直角三角形的重心 详细说明或证明 急 360问答


新網頁1


重心列表 维基百科 自由的百科全书



M Sudo S Room 円弧 及び 扇形の重心


質問です 扇形の重心の位置を求めなさい これについて回答お願いします Yahoo 知恵袋
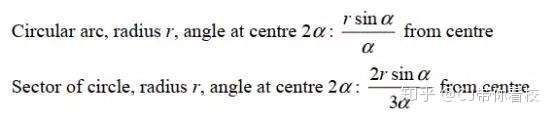


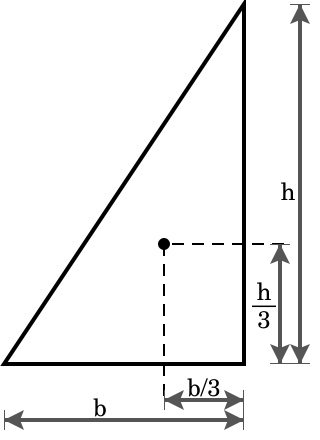
考前抢分专栏 A Level数学m2关键考点及易错点总结 知乎


圓心角所對弦長 弧長與扇形面積 Live 多媒體數學觀念典online


扇形の重心 物理実験集 管理人の近況報告ブログ



重心列表 维基百科 自由的百科全书


面的重心求法


一 与圆有关的各种图形的面积 几何重心与转动惯量计算公式



清水 団 Dan Shimizu Op Twitter 扇形の重心の求め方です


平面図形の面積 A 周長 L および重心位置 G 扇形 P11



御所実業高校 機械工学科 の日記 第22回 重心の答え合わせ


3 5 重心 形心和静矩



重心列表 维基百科 自由的百科全书



Fzu 1330 Center Of Gravity 计算几何 求扇形重心 It610 Com


3 5 重心 形心和静矩


扇形计算公式 钢筋计算公式 光通量计算公式 箍筋长度计算公式 Www Shianwang Com



扇形の重心を積分で ウソの国 詩と宗教 St5402jp
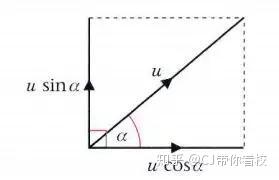


考前抢分专栏 A Level数学m2关键考点及易错点总结 知乎



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积



弧长和扇形的面积红寺堡二中马建鹏 Ppt Download


直角梯形形心公式图片 第1页 要无忧健康图库


传统射箭的站姿选择 1 手战堂射箭录 新浪博客



Cnb 一种柴油机曲柄惯量柔性平衡装置及其设计方法 Google Patents


扇形重心位置计算 三人行教育网 Www 3rxing Org
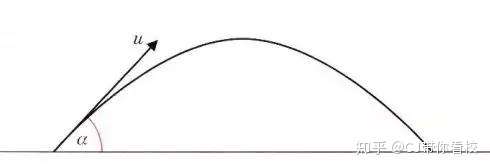


考前抢分专栏 A Level数学m2关键考点及易错点总结 知乎


平面図形の面積 A 周長 L および重心位置 G 弓形 P11



No comments:
Post a Comment